An example of model generation illustrated with a linear regression

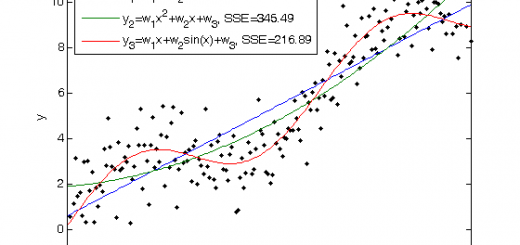
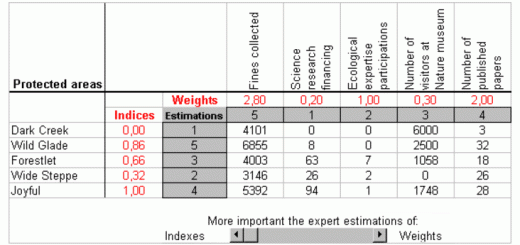
The problem of model generation is illustrated with a linear regression model of a single variable. See the example.

Contents

Make synthetic data using a model from generated set

To make such data we must assign a model and its parameters, set the independent variable and the calculate dependent variable.

f = inline('w(1)*x.^0 + w(2)*x.^(1/2) + w(3)*x.^1', 'w','x'); % model
w = [1 -2 2]'; % parameters
x = [0.1:0.1:1]'; % independent variable
y = f(w,x); % dependent variable
h = figure; hold on
plot(x,y,'*');

Assign set of the primitive functions

Assume the intended model is a linear combination of the primitive functions

g{1} = 'x.^0';
g{2} = 'x.^(1/2)';
g{3} = 'x.^1';
g{4} = 'x.^(3/2)';
g{5} = 'x.^log(x)';
g

g = 

    'x.^0'    'x.^(1/2)'    'x.^1'    'x.^(3/2)'    'x.^log(x)'

Make the exhaustive search in the set of the models

Now we have 2^5-1 models.

% each element  of the boolean vector defines is a primitive in the model of
% not
cnt = zeros(1,length(g)); % boolean vector
ErrList = []; % keep errors of the model;
CntList = []; % keep model descriptions
for k = 1:2^length(g)-1 % for each model
    cnt = cntbin(cnt); % make a model description
    [X, f] = makelinmodel(g, cnt, x); % create a model
    w = pinv(X'*X)*X'*y;   % tune parameters by Least Squares
    err = sumsqr(f(w,x)-y); % SSE, sum of square error
    % store the results
    ErrList = [ErrList err];
    CntList = [CntList; cnt];
end

Select the best model according to its SSE

Consider a model of the best structure has minimal SSE

[dummy, idx] = min(ErrList); % find minimal SSE
cnt = CntList(idx,:); % make the model description
[X, f] = makelinmodel(g, cnt, x); % create the model
w = pinv(X'*X)*X'*y; % tune parameters
plot(x, f(w,x),'r-'); % plot results
xlabel('\xi');
ylabel('y');
legend('data', 'model');

f

f =

     Inline function:
     f(w,x) = w(1)*x.^0+w(2)*x.^(1/2)+w(3)*x.^1

Appendix 1, makelinmodel.m

% function [X, f] = makelinmodel(g, cnt, x)
% % make a linear model as an inline function and a matrix
% % [X, f] = makelinmodel(cnt, g, x);
% %
% % g {string array 1,L} library of primitive functions
% % cnt [1,L] binary counter 1 means the primitive in in the model
% % x [m,1] data vector
% % X [m,L] output matrix for the model, y = Xw
% % f = f(w,x) a model function for linear regression
% %
% % Example
% % g = {'x.^0', 'x.^1'}; % the primitive functions
% % cnt = [1 1]; % include both function on the model
% % x = rand(8, 1); % a column vector
% % [X, f] = makelinmodel(g, cnt, x)
% % y = f(ones(1,length(cnt)),x)
%
% X = []; % matrix y = Xw for the normal equation of the linear regression
% str=''; % string to make a model (linear combination)
% idx= 0; % number of item in the linear combination
% for j = 1:length(cnt) %
%    if cnt(j)
%       X = [X eval(g{j})]; % add a column to matrix
%       idx = idx+1; % increase index of the weight
%       str = [str, 'w(', num2str(idx), ')*', g{j} ,'+']; % concatenate the model string
%    end
% end
%
% if length(str)>1,
%     f = inline(str(1:end-1),'w','x'); % make the regression model
% end
% return

Appendix 2, cntbin.m

% function c = cntabover(c,a,b)
% %
% % c = cntbin(c)
% %
% % Vector of digits of a binary number plus one
% %
% % Example:
% %  c = zeros(1,4);
% %  for i=1:2^length(c)-1
% %    c = cntbin(c)
% %  end
% %
% % returns
% % c =
% %      0     0     0     1
% %      0     0     1     0
% %     ...
% %      1     1     1     0
% %      1     1     1     1
%
%
%
% i = length(c);
% while i > 0
%     if c(i)+1 <= 1
%          c(i) = c(i)+1;
%          break
%     else
%         c(i) = 0;
%         i=i-1;
%     end
% end
% return