Difference between revisions of "Functional data analysis for BCI and biomedical signals"
| (24 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{#seo: | ||
| + | |title=BCI forecasting models | ||
| + | |titlemode=replace | ||
| + | |keywords=BCI | ||
| + | |description=My research focuses on the construction of BCI forecasting models. I use deep learning models. The main challenges of the study are phase space construction, dimensionality reduction, manifold learning, heterogeneous modeling, and knowledge transfer. | ||
| + | }} | ||
''[[Vadim]]'', 2023 | ''[[Vadim]]'', 2023 | ||
| − | Brain-computer interfaces require a sophisticated forecasting model. This model | + | Brain-computer interfaces require a sophisticated forecasting model. This model fits heterogeneous data. The signals come from ECoG, ECG, fMRI, hand and eye movements, and audio-video sources. The model must reconstruct hidden dependencies in these signals and establish relations between brain signals and limb motions. My research focuses on the construction of BCI forecasting models. I use deep learning models. The main challenges of the study are phase space construction, dimensionality reduction, manifold learning, heterogeneous modeling, and knowledge transfer. Since the measured data are stochastic and contain errors, I actively use and develop Bayesian model selection methods. These methods infer criteria to optimize model structure and parameters. They aim to select an accurate and robust BCI model. |
| − | |||
| − | |||
== Brain signals and dimensionality reduction == | == Brain signals and dimensionality reduction == | ||
| − | + | Intracranial electroencephalography [1] signals are tensors or time-related tensor fields. They have several indexes for physical space, time, and frequency. The multi-index structure of time series causes redundancy of space features and multi-correlation [2]. It turns out to increase the complexity of the model and obtain unstable forecasts [3]. I address the dimensionality reduction problem for high-dimensional data. The essential methods are tensor and high-order singular value decomposition [4]. We proposed a feature selection method to reveal hidden dependencies in data [5]. It minimizes multi-correlation in the source space and maximizes the relation between source and target spaces. This solution shrinks the number of model parameters tenfold and stabilizes the forecast. To boost the accuracy, I plan to investigate dimensionality reduction. I consider deep learning models in discrete time: the stacks of autoencoders and recurrent neural networks, and in continuous time: the neural ordinal differential equations [6]. | |
| − | Intracranial electroencephalography | ||
| − | |||
== Biomedical signal decoding and multi-modeling == | == Biomedical signal decoding and multi-modeling == | ||
| + | The BCI models are the signal decoding models [7]. It is a special class of models that includes canonical correlation analysis for multivariate and tensor variables. I plan to study the problem of model selection to restore hidden dependencies in the source and target spaces. For example, periodical limb movements cause multiple correlations in the target space. We proposed to reduce the dimension by projecting the source and target in the latent space [8]. Linear and non-linear methods match predictive models in high-dimensional spaces [9]. Recently we proposed a feature selection algorithm for linear models and tested it on ECoG signals [2]. I plan to develop this algorithm for tensor dimensionality reduction. The base method is the High-order partial least squares [7]. A good problem for development is manifold learning. The manifold is a solution to the neural partial differential equations [10]. The challenge is to find an optimal dimensionality of the manifold. | ||
| + | <!--~\citep{lauzon2018sequential,engel2017kernel,biancolillo2017extension,hervas2018sparse}--> | ||
| + | ==Heterogeneous data and knowledge transfer== | ||
| + | The new studies of brain activity fruitfully deliver a variety of measurements. For a group of patients, they contain audio, video, iEEEG-ECoG, ECG, fMRI, and hand or eye movements. These data sets require multi models. Each patient has its peculiarities. It requires a method to transfer knowledge from one patient's model to another. Knowledge transfer for heterogenous models is an important part of my investigation. I use Bayesian inference for multimodel selection to construct an ensemble of models and teacher-student pairs. The information, gained by the properly trained models serves as a prior distribution for a student model. | ||
== Continous-time physical activity recognition == | == Continous-time physical activity recognition == | ||
| + | A forecast of limb motions stands on cycles of motion [14]. They form a phase trajectory [15]. Parameters of the trajectory define a class of motion. A sequence of these classes forms the physical human behavior pattern. Recently we proposed human activity recognition algorithm based on the data from wearable sensors [16]. The solution is based on the hierarchical representation of activities as sets of low-level motions. The hierarchical model provides an interpretable description of studied motions. | ||
| + | ==Functional data analysis== | ||
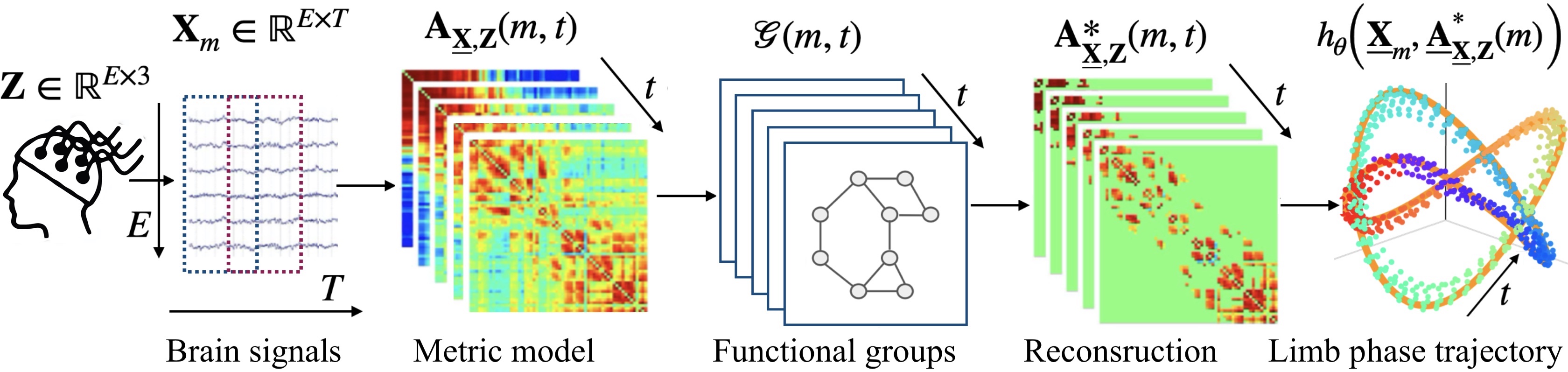
| + | The methods of functional brain mapping verify the signal diffusion hypothesis. It shows that activity zone changes over the cortical space control limb movements [17]. The model must consider the spatial structure of the signals. Neural networks do not consider information about the neighborhood on the brain surface. We proposed a graph representation of brain signals. It reveals interrelationships of different areas and provides a neurobiological interpretation of the functional connections. I plan to develop various methods for constructing a connectivity matrix that defines a graph structure. Estimating connectivity relies on correlation, spectral analysis, and canonic correlation analysis. The matrix is a metric tensor that defines a Riemannian space. The forecasting model is a composition of a graph convolution for aggregating spatial information and a recurrent or neural ODE model [18]. | ||
| + | [[File:BCI_graph.jpeg|class=img-responsive|left|Brain functional group reconstruction model]] | ||
| − | == | + | ==Direction of future work== |
| − | + | The Deep Learning methods give immediate results in modeling. They bring forecasts to compare with and develop. A promising field of research is Functional Data Analysis. It works with objects and spaces of infinite dimensionality. Geometric Deep Learning [19] connects the physical nature of measurements and the axioms to construct forecasting models. It brings physics-informed neural networks [20]. I believe combining modern Deep Learning techniques with Advanced Calculus and Physics delivers fruitful results in practical applications of BCI and biomedical signal analysis. | |
| − | + | ==References== | |
| − | == | + | # Maryam Bijanzadeh, Ankit N. Khambhati, Maansi Desai, Deanna L. Wallace, Alia Shafi, Heather E. Dawes, Virginia E. Sturm, and Ed- ward F. Chang. Decoding naturalistic affective behaviour from spectro-spatial features in multi-day human iEEG. Nature Human Behaviour, 6(6):823–836, 2022. |
| − | + | # A. P. Motrenko and V. V. Strijov. Multi-way feature selection for Ecog-based brain-computer interface. Expert Systems with Applications, 114(30):402–413, 2018. | |
| − | + | # A. M. Katrutsa and V. V. Strijov. Stresstest procedure for feature selection algorithms. Chemometrics and Intelligent Laboratory Systems, 142:172–183, 2015. | |
| − | + | # Tamara G. Kolda and Brett W. Bader. Tensor decompositions and applications. SIAM Review, 51(3):455–500, 2009. | |
| − | + | # A. M. Katrutsa and V. V. Strijov. Comprehensive study of feature selection methods to solve multicollinearity problem according to evaluation criteria. Expert Systems with Applications, 76:1–11, 2017. | |
| − | + | # Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David Duvenaud. Neural ordinary differential equations. Advances in Neural Information Processing Systems 31, 2018. | |
| + | # Qibin Zhao, C. F. Caiafa, D. P. Mandic, Z. C. Chao, Y. Nagasaka, N. Fujii, Liqing Zhang, and A. Cichocki. Higher order partial least squares (HOPLS): A generalized multilinear regression method. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(7):1660–1673, 2013. | ||
| + | # R. V. Isachenko and V. V. Strijov. Quadratic programming feature selection for multicorrelated signal decoding with partial least squares. Expert Systems with Applications, 207:117967, 2022. | ||
| + | # R. V. Isachenko and V. V. Strijov. Quadratic programming optimization with feature selection for non-linear models. Lobachevskii Journal of Mathematics, 39(9):1179–1187, 2018. | ||
| + | # Jiequn Han, Arnulf Jentzen, and Weinan E. Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences, 115(34):8505–8510, 2018. | ||
| + | # Julia Berezutskaya, Mariska J. Vansteensel, Erik J. Aarnoutse, Zachary V. Freudenburg, Giovanni Piantoni, Mariana P. Branco, and Nick F. Ramsey. Open multimodal iEEG-fMRI dataset from naturalistic stimulation with a short audiovisual film. Scientific Data, 9(1), 2022. | ||
| + | # A. V. Grabovoy and V. V. Strijov. Prior distribution selection for a mixture of experts. Computational Mathematics and Mathematical Physics, 61(7):1149–1161, 2021. | ||
| + | # O. Y. Bakhteev and V. V. Strijov. Comprehensive analysis of gradient-based hyper-parameter optimization algorithms. Annals of Operations Research, pages 1–15, 2020. | ||
| + | # A. P. Motrenko and V. V. Strijov. Extracting fundamental periods to segment human motion time series. IEEE Journal of Biomedical and Health Informatics, 20(6):1466–1476, 2016. | ||
| + | # A. Motrenko et. al. Continuous physical activity recognition for intelligent labour monitoring. Multimedia Tools and Applications, 81(4):4877–4895, 2021. | ||
| + | # A. V. Grabovoy and V. V. Strijov. Quasi-periodic time series clustering for human activity recognition. Lobachevskii Journal of Mathematics, 41:333–339, 2020. | ||
| + | # Alim Louis Benabid et al. An exoskeleton controlled by an epidural wireless brain–machine interface in a tetraplegic patient: a proof-of-concept demonstration. The Lancet Neurology, 18(12):1112–1122, 2019. | ||
| + | # David K. Duvenaud Yulia Rubanova, Ricky T. Q. Chen. Latent ordinary differential equations for irregularly-sampled time series. Advances in Neural Information Processing Systems 32, 2019. | ||
| + | # Michael M. Bronstein, Joan Bruna, Taco Cohen, and Petar Veliˇckovi ́c. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges, 2021. | ||
| + | # M. Raissi, P. Perdikaris, and G.E. Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019. | ||
Latest revision as of 22:21, 11 February 2024
Vadim, 2023
Brain-computer interfaces require a sophisticated forecasting model. This model fits heterogeneous data. The signals come from ECoG, ECG, fMRI, hand and eye movements, and audio-video sources. The model must reconstruct hidden dependencies in these signals and establish relations between brain signals and limb motions. My research focuses on the construction of BCI forecasting models. I use deep learning models. The main challenges of the study are phase space construction, dimensionality reduction, manifold learning, heterogeneous modeling, and knowledge transfer. Since the measured data are stochastic and contain errors, I actively use and develop Bayesian model selection methods. These methods infer criteria to optimize model structure and parameters. They aim to select an accurate and robust BCI model.
Contents
Brain signals and dimensionality reduction
Intracranial electroencephalography [1] signals are tensors or time-related tensor fields. They have several indexes for physical space, time, and frequency. The multi-index structure of time series causes redundancy of space features and multi-correlation [2]. It turns out to increase the complexity of the model and obtain unstable forecasts [3]. I address the dimensionality reduction problem for high-dimensional data. The essential methods are tensor and high-order singular value decomposition [4]. We proposed a feature selection method to reveal hidden dependencies in data [5]. It minimizes multi-correlation in the source space and maximizes the relation between source and target spaces. This solution shrinks the number of model parameters tenfold and stabilizes the forecast. To boost the accuracy, I plan to investigate dimensionality reduction. I consider deep learning models in discrete time: the stacks of autoencoders and recurrent neural networks, and in continuous time: the neural ordinal differential equations [6].
Biomedical signal decoding and multi-modeling
The BCI models are the signal decoding models [7]. It is a special class of models that includes canonical correlation analysis for multivariate and tensor variables. I plan to study the problem of model selection to restore hidden dependencies in the source and target spaces. For example, periodical limb movements cause multiple correlations in the target space. We proposed to reduce the dimension by projecting the source and target in the latent space [8]. Linear and non-linear methods match predictive models in high-dimensional spaces [9]. Recently we proposed a feature selection algorithm for linear models and tested it on ECoG signals [2]. I plan to develop this algorithm for tensor dimensionality reduction. The base method is the High-order partial least squares [7]. A good problem for development is manifold learning. The manifold is a solution to the neural partial differential equations [10]. The challenge is to find an optimal dimensionality of the manifold.
Heterogeneous data and knowledge transfer
The new studies of brain activity fruitfully deliver a variety of measurements. For a group of patients, they contain audio, video, iEEEG-ECoG, ECG, fMRI, and hand or eye movements. These data sets require multi models. Each patient has its peculiarities. It requires a method to transfer knowledge from one patient's model to another. Knowledge transfer for heterogenous models is an important part of my investigation. I use Bayesian inference for multimodel selection to construct an ensemble of models and teacher-student pairs. The information, gained by the properly trained models serves as a prior distribution for a student model.
Continous-time physical activity recognition
A forecast of limb motions stands on cycles of motion [14]. They form a phase trajectory [15]. Parameters of the trajectory define a class of motion. A sequence of these classes forms the physical human behavior pattern. Recently we proposed human activity recognition algorithm based on the data from wearable sensors [16]. The solution is based on the hierarchical representation of activities as sets of low-level motions. The hierarchical model provides an interpretable description of studied motions.
Functional data analysis
The methods of functional brain mapping verify the signal diffusion hypothesis. It shows that activity zone changes over the cortical space control limb movements [17]. The model must consider the spatial structure of the signals. Neural networks do not consider information about the neighborhood on the brain surface. We proposed a graph representation of brain signals. It reveals interrelationships of different areas and provides a neurobiological interpretation of the functional connections. I plan to develop various methods for constructing a connectivity matrix that defines a graph structure. Estimating connectivity relies on correlation, spectral analysis, and canonic correlation analysis. The matrix is a metric tensor that defines a Riemannian space. The forecasting model is a composition of a graph convolution for aggregating spatial information and a recurrent or neural ODE model [18].
Direction of future work
The Deep Learning methods give immediate results in modeling. They bring forecasts to compare with and develop. A promising field of research is Functional Data Analysis. It works with objects and spaces of infinite dimensionality. Geometric Deep Learning [19] connects the physical nature of measurements and the axioms to construct forecasting models. It brings physics-informed neural networks [20]. I believe combining modern Deep Learning techniques with Advanced Calculus and Physics delivers fruitful results in practical applications of BCI and biomedical signal analysis.
References
- Maryam Bijanzadeh, Ankit N. Khambhati, Maansi Desai, Deanna L. Wallace, Alia Shafi, Heather E. Dawes, Virginia E. Sturm, and Ed- ward F. Chang. Decoding naturalistic affective behaviour from spectro-spatial features in multi-day human iEEG. Nature Human Behaviour, 6(6):823–836, 2022.
- A. P. Motrenko and V. V. Strijov. Multi-way feature selection for Ecog-based brain-computer interface. Expert Systems with Applications, 114(30):402–413, 2018.
- A. M. Katrutsa and V. V. Strijov. Stresstest procedure for feature selection algorithms. Chemometrics and Intelligent Laboratory Systems, 142:172–183, 2015.
- Tamara G. Kolda and Brett W. Bader. Tensor decompositions and applications. SIAM Review, 51(3):455–500, 2009.
- A. M. Katrutsa and V. V. Strijov. Comprehensive study of feature selection methods to solve multicollinearity problem according to evaluation criteria. Expert Systems with Applications, 76:1–11, 2017.
- Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David Duvenaud. Neural ordinary differential equations. Advances in Neural Information Processing Systems 31, 2018.
- Qibin Zhao, C. F. Caiafa, D. P. Mandic, Z. C. Chao, Y. Nagasaka, N. Fujii, Liqing Zhang, and A. Cichocki. Higher order partial least squares (HOPLS): A generalized multilinear regression method. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(7):1660–1673, 2013.
- R. V. Isachenko and V. V. Strijov. Quadratic programming feature selection for multicorrelated signal decoding with partial least squares. Expert Systems with Applications, 207:117967, 2022.
- R. V. Isachenko and V. V. Strijov. Quadratic programming optimization with feature selection for non-linear models. Lobachevskii Journal of Mathematics, 39(9):1179–1187, 2018.
- Jiequn Han, Arnulf Jentzen, and Weinan E. Solving high-dimensional partial differential equations using deep learning. Proceedings of the National Academy of Sciences, 115(34):8505–8510, 2018.
- Julia Berezutskaya, Mariska J. Vansteensel, Erik J. Aarnoutse, Zachary V. Freudenburg, Giovanni Piantoni, Mariana P. Branco, and Nick F. Ramsey. Open multimodal iEEG-fMRI dataset from naturalistic stimulation with a short audiovisual film. Scientific Data, 9(1), 2022.
- A. V. Grabovoy and V. V. Strijov. Prior distribution selection for a mixture of experts. Computational Mathematics and Mathematical Physics, 61(7):1149–1161, 2021.
- O. Y. Bakhteev and V. V. Strijov. Comprehensive analysis of gradient-based hyper-parameter optimization algorithms. Annals of Operations Research, pages 1–15, 2020.
- A. P. Motrenko and V. V. Strijov. Extracting fundamental periods to segment human motion time series. IEEE Journal of Biomedical and Health Informatics, 20(6):1466–1476, 2016.
- A. Motrenko et. al. Continuous physical activity recognition for intelligent labour monitoring. Multimedia Tools and Applications, 81(4):4877–4895, 2021.
- A. V. Grabovoy and V. V. Strijov. Quasi-periodic time series clustering for human activity recognition. Lobachevskii Journal of Mathematics, 41:333–339, 2020.
- Alim Louis Benabid et al. An exoskeleton controlled by an epidural wireless brain–machine interface in a tetraplegic patient: a proof-of-concept demonstration. The Lancet Neurology, 18(12):1112–1122, 2019.
- David K. Duvenaud Yulia Rubanova, Ricky T. Q. Chen. Latent ordinary differential equations for irregularly-sampled time series. Advances in Neural Information Processing Systems 32, 2019.
- Michael M. Bronstein, Joan Bruna, Taco Cohen, and Petar Veliˇckovi ́c. Geometric deep learning: Grids, groups, graphs, geodesics, and gauges, 2021.
- M. Raissi, P. Perdikaris, and G.E. Karniadakis. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378:686–707, 2019.