Least angle regression (LARS)

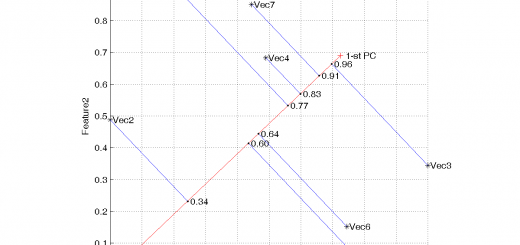
LARS is one of the most effective algorithms to select linear regression models. It is not so greedy as step-wise regression and takes not so much steps as Lasso.

Contents

% Least Angle Regression, demo

Create synthetic data

We think of a model, see below the code. Try to guess the model with LARS.

% Assign a model
f = inline('w(1)*x.^0 + w(2)*x.^(1/2) + w(3)*x.^1', 'w','x'); % synthetic model
b = [1 -2 2]'; % parameters
x = [0.1:0.1:1]'; % independent variable
y = f(b,x); % dependent variable

% We use the following features to find the model we thought of
g = {'x.^0', 'x.^(1/2)', 'x.^1', 'x.^(3/2)', 'x.*log(x)'};
% make the sample set; columns are independent variables
X = eval([ '[' g{1} ' ' g{2} ' ' g{3} ' ' g{4} ' ' g{5} ']']);

Run LARS

[n,p] = size(X);
muA = zeros(n,1);  % estimation of the dependent variable
beta = zeros(p,1); % estimation of parameters
betaLtst = beta';  % keep parameters in a storage

for i = 1:p
    % correlation coefficients between each feature (column of X) and vector of residuals
    c = X'*(y-muA); % note that columns of X are centered and normalized
    [C, A] = max(abs(c)); % find maximal value of correlation and corresponding index j of column in X
    % A = find(C == abs(c));
    % Aplus = find(C==c); % never used
    Sj  = sign(c(A)); % get sign of j-th correlation coefficient
    XA = X(:,A).*(ones(n,1)*Sj'); %
    % XA = X(:,A)*Sj; %
    G = XA'*XA; % norm of XA
    oA = ones(1,length(A)); % vector of ones
    AA =(oA*G^(-1)*oA')^(-0.5); % inverse matrix in the normal equation

    wA = AA*G^(-1)*oA'; % parameters to compute the unit bisector
    uA = XA*wA; % compute the unit bisector
    a = X'*uA; % product vector to compute new gamma
    if i<p % for all columns of X but the last
        M = [(C-c)./(AA-a);(C+c)./(AA+a)];
        M(find(M<=0)) = +Inf;
        gamma = min(M);
    else
        gamma  = C/AA;
    end

    muA = muA + gamma*uA; % make new approximation of the dependent variable
    beta(A) = beta(A) + gamma*wA.*Sj; % make new parameters
    betaLtst = [betaLtst; beta']; % store the parameters at k-th step
end

Plot parameters at each step of LARS

s1 = sum(abs(betaLtst),2);
plot(s1, betaLtst);
hold on
plot(s1, betaLtst);
xlabel('sum of model parameters');
ylabel('parameters');
legend('\beta_3', '\beta_1', '\beta_2')
hold off

Plot the results

idx = find(beta ~= 0);
disp('Recovered model contains')
g(idx)

% Recover LARS results using the last value of beta
y1 = X(:,idx)*beta(idx);

% Recover Least Squares result
Xa = X(:,idx);
y3 = Xa * pinv(Xa'*Xa)*Xa'*y;

plot(x,y,'*');
hold on
plot(x,y1,'r-');
plot(x,y3,'b-');
legend('Source data','LARS C_p metric', 'LARS selected')

Recovered model contains

ans = 

    'x.^0'    'x.^(1/2)'    'x.^1'

Warning

% Note that Least Squares
w = pinv(X'*X)*X'*y
% give the same result (for this very example, of course)

w =

    1.0000
   -2.0000
    2.0000
    0.0000
   -0.0000