Principal Component Analysis

Plot the 1st Principal Component of the 2D sample set. The script uses a standard 1PC procedure and do not canter the matrix as it recommnded.

Contents

Get the data

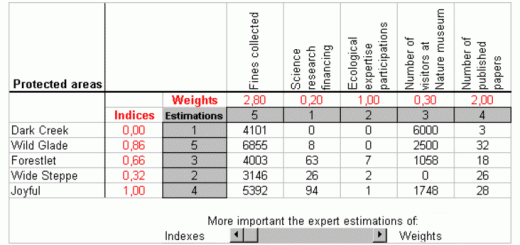
The matrix A has objects in its rows and features (the function princomp uses this feature )

A =[
    2.66   30.00
    1.00   44.63
    3.00   40.33
    1.98   50.50
    1.23   60.00
    2.49   34.55
    1.89   55.50
    ];
[m,n]=size(A);

Normalize the matrix

In real projects it is needed to descale the data. Be careful, this precedure is not robust to outlier objects.

for j = 1:n
    A(:,j)=( A(:,j)-min(A(:,j)) ) / ( max(A(:,j))-min(A(:,j)) );
end

% center the matrix, since the embedded princomp centers the matrix any way
%for j = 1:n, A(:,j)=A(:,j)-mean(A(:,j)); end

Caclulate the Singular Values Decomposition

[U,L,V] = svd(A); % put in 1/sqrt(n-1) later

pc1 = V(:,1);% pc1 is the first right singular vector of A
% so the principal components are the rows of the matrix A
% the Matlab procedure 'princomp' center the matrix and then makes svd
% coeff of the 'princomps' are the matrix V.

norm_pc1 = pc1'*pc1; % just check it
if (norm_pc1-1.0>1e-10), error('Norm of the 1PC is not 1!'); end

Calculate projections

pr = [ A * pc1 .* pc1(1), A * pc1 .* pc1(2)]; % calculate projections

q = sqrt(sum(pr.*pr,2)); % caclulate norms of projections, so-called integral indicators

Check the residuals

Z = A*V;
[q - abs(Z(:,1)) < 1e-10]'

% q % the distance to the projections are equal to Z (rotated coordinates)
% abs(Z(:,1))

ans =

     1     1     1     1     1     1     1

Plot the raw vectors projection to the 1-st PC

h = figure; % create a new figure
xlabel Feature1
ylabel Feature2
set(gca,'PlotBoxAspectRatio',[1 1 1]'); % set 1:1 axis aspect ratio
grid on % show the axis grid
%plot([0,1,1,0,0],[0,0,1,1,0],'-g'); % green square [0,1]x[0,1];
hold on % keep all the painting on
plot(A(:,1),A(:,2),'*k'); % plot the objects with asterisks
% plot objects names (order numbers)
for i = 1:m, text(A(i,1),A(i,2),[' Vec',num2str(i)]); end

plot(-pc1(1),-pc1(2),'+r'); % the 1-st  PC, vector
plot([0,-pc1(1)],[0,-pc1(2)],'-r'); % the same, plot a line from (0.0) to th 1PC
text(-pc1(1),-pc1(2),'  1-st PC'); % show the text about it

for i=1:m % m objects to plot
    % TO DO
    plot([A(i,1),pr(i,1)],[A(i,2),pr(i,2)],'b-');
    text(pr(i,1),pr(i,2),sprintf(' %0.2f',q(i)));
    plot(pr(i,1),pr(i,2),'.k');
end
title('1-st Principal Component');
%saveas(h, 'demo_principal_component_1','png')
close(h);

http://strijov.com

% this file: demo_principal_component